2.2. La démonstration dans les sciences formelles
la démarche hypothético-déductive dans les mathématiques
Les mathématiques (ainsi que la logique) découvre des vérités grâce à la seule raison. Il s’agit de vérités formelles (ou vérités de raison), qui reposent sur la cohérence de systèmes de pensée (par exemple la géométrie euclidienne, avec ses définitions, postulats, théorèmes).
Les vérités mathématiques s’opposent aux vérités empiriques des sciences expérimentales car elles ne décrivent pas des êtres existants dans la nature. Ce sont des idées, des inventions de l’esprit : le cercle ne désigne pas un objet existant dans la nature, les nombres, le point ou la ligne sans épaisseur non plus.
Pour démontrer ses connaissances, les mathématiques utilisent le raisonnement par déduction. Les propositions sont déduites de propositions antérieures suivant un raisonnement logique. Démontrer en mathématiques, c’est donc partir d’idées générales considérées comme vraies, puis en déduire d’autres idées.
Ces premières vérités générales à partir desquelles les mathématiciens font des démonstrations sont de deux ordres : axiomes et postulats.
- Les axiomes sont des vérités logiques s’imposant par leur évidence absolue, mais que l’on ne peut pas démontrer. Par exemple : « Le tout est plus grand que la partie » ou encore « 2 quantités égales à une 3e sont égales entre elles ».
- Les postulats sont des propositions que l’on n’arrive pas encore à démontrer et que le mathématicien demande à son auditeur de lui accorder. Ainsi, Euclide pose comme un postulat que « par un point pris hors d’une droite dans un plan, on ne peut mener qu’une parallèle à cette droite » (Vème postulat d’Euclide). Le postulat ne peut pas être démontré (contrairement aux théorèmes).
Les géométries non-euclidiennes
Ce Vème postulat d’Euclide est contredit au 19e s. par un savant russe (Lobatchevski) qui suppose que l’on pourrait mener plusieurs parallèles à une droite donnée passant par un même point (une infinité de non-sécantes). De cette hypothèse non-euclidienne, Lobatchevski déduit un ensemble de théorèmes non contradictoires et il construit une géométrie cohérente, dans laquelle l’espace contient une infinité de dimensions, alors que celui d’Euclide en contient 3. Riemann, un autre mathématicien, imagine une autre géométrie non-euclidienne, dans laquelle l’espace sphérique contient 0 dimensions. Dans ce système, il ne passe aucune droite parallèle à une première.
| Géométrie euclidienne | Géométrie de Lobatchevski | Géométrie de Riemann |
|---|---|---|
 |  |  |
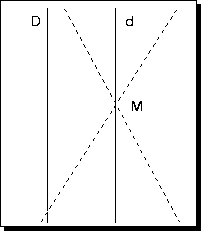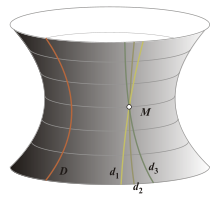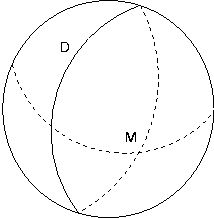| La droite d est la seule droite passant par le point M et parallème à la droite D. | Il existe une infinité de droites qui, comme d1, d2 et d3, passent par le point M et sont parallèles à la droite D. | Il n’existe aucune droite passant par le point M et parallèle à la droite D. |
Les sciences mathématiques sont donc hypothético-déductives : le mathématicien se donne un système de définitions et d’axiomes et il déduit de ces « hypothèses » une série de conséquences.